أساسيات أنظمة العد / الترقيم - Numbering Systems
مقدمة لـ الأنظمة العددية - أنظمة الترقيم، وما هي مكونات أي نظام عددي، وكيف يتم تمثيل الأرقام في أنظمة العد المختلفة؟ و أهم الأنظمة العددية المستخدمة في علوم الحاسب، وشرح مبسط لنظام العد العشري، وسوف نتعرف على القاعدة العامة لـ تحويل أي رقم من أي نظام عددي إلى نظام العد العشري، وتحويل أي عدد عشري إلى أي نظام عد آخر (ثنائي - ثماني - سادس عشري).
ما هي الأنظمة العددية؟
أحيانا تسمى بالعربية أنظمة الترقيم أو نظام الأرقام وبالإنجليزية يمكن تسميتها Numbering Systems أو Numeral Systems أو Counting Systems وكلها مصطلحات تدل على نفس المعنى.
ويمكن تعريف الأنظمة العددية على أنها طريقة لتمثيل (كتابة أو عرض) الأرقام برموز محددة حتى نتمكن من التعبير عن قيمتها وإجراء العمليات الحسابية عليها.
يعتبر نظام العد العشري Decimal Numeral System من أشهر أنواع الأنظمة العددية، التى لاقت قبولا للإستخدام بين البشر لقرون طويلة، وإذا بحثت في تاريخ البشرية سوف تجد أن هناك العديد من الأنظمة العددية التي تم إبتكارها وإستخدامها على مر العصور في الكثير من الحضارات (مثل: الفراعنة، المايا، الرومان، العرب، ...).
ما هي مكونات أي نظام عددي؟
يتكون أي نظام عددي من مجموعة محددة من الرموز - Symbols، والتي تستخدم لتمثيل أي رقم في هذا النظام العددي، ويحتوي أيضا كل نظام عددي على ما يعرف بـ رقم الأساس وهو المعروف بالإنجليزية بـ Base وأحيانا يسمى Radix، ويتم تحديد رقم الأساس الخاص بالنظام العددي على حسب عدد الرموز المستخدمة في تمثيل (كتابة) الأعداد في هذا النظام العددي.
والجدول التالي يوضح الأنظمة العددية الأكثر إستخداما والرموز المستخدمة في تمثيل كل نظام عددي، ورقم الأساس الخاص بكل نظام
| النظام العددي | رقم الأساس | الرموز - Symboles |
|---|---|---|
| النظام العشري Decimal | 10 | 0 - 1 - 2 - 3 - 4 - 5 - 6 - 7 - 8 - 9 |
| النظام الثنائي Binary | 2 | 0 - 1 |
| النظام الثماني Octal | 8 | 0 - 1 - 2 - 3 - 4 - 5 - 6 - 7 |
| النظام السادس عشر Hexadecimal | 16 | 0 - 1 - 2 - 3 - 4 - 5 - 6 - 7 - 8 - 9 - A - B - C - D - E - F |
الأرقام - الأعداد
الرقم أو العدد هو عبارة عن مجموعة من الخانات بحيث تحتوي كل خانة على رمز واحد فقط، وتختلف قيمة (وزن) الرمز بإختلاف الخانة التي يكتب بها.
ويسمى النظام الذي يعمل بهذه الطريقة بـ نظام العد الموضعي أو المكاني أو بالإنجليزية Positional Numbering System.
ولذلك سوف تلاحظ أنه في نظام العد السادس عشر قمنا بإستخدام الرموز (A, B, C, D, E, F) لتمثل الأرقام على التولي (10, 11, 12, 13, 14, 15)، حيث لا يمكننا إستخدام رمز مزدوج في خانة واحدة.
ولكي تتمكن من فهم المقصود بنظام العد الموضعي سوف نستخدم مثال من النظام العشري، ولنأخذ على سبيل المثال الرقم 11.1، سوف تلاحظ أننا قمنا بإستخدام رمز واحد فقط وهو الرمز "1" لكي نقوم بتمثيل العدد أحد عشر و واحد من عشرة.
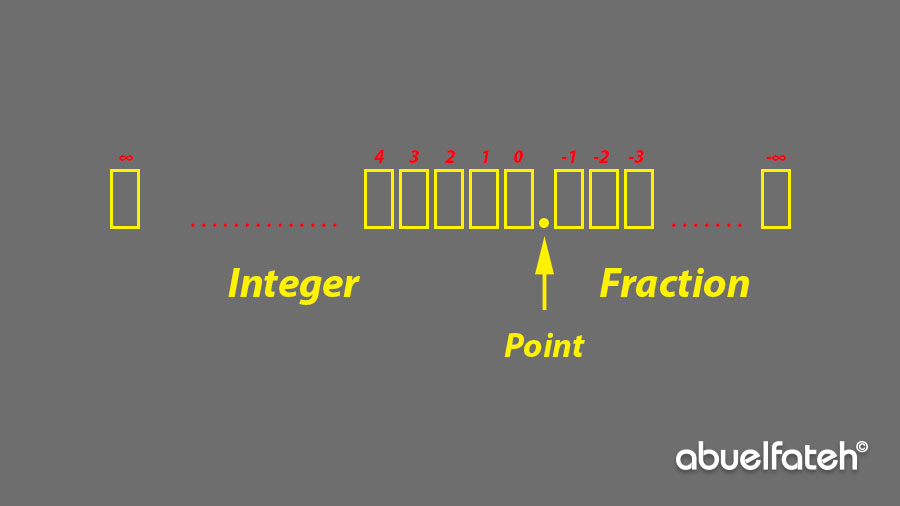
وفي هذا المثال يتكون الرقم من قسمين وهما الرقم الصحيح (Integer) والرقم العشري أو الكسري (Fraction) ويفصل بينهما العلامة أو رمز النقطة . وهو الرمز الأكثر إستخداما، وفي اللغة العربية (رموز الأرقام العربية) يتم إستخدام علامة الفاصلة ,، بحيث يكون الرقم الصحيح على يسار العلامة والرقم الكسري على يمين العلامة.
ومن المثال، الرمز "1" على يمين العلامة يمثل عُشر الرقم (واحد على عشرة)، والرقم الصحيح مكون من خانتين، خانة على اليمين وهي خانة الآحاد وقيمة الرمز "1" هي واحد، وخانة العشرات وهنا الرمز "1" يحمل القيمة عشرة، ومن ذلك سوف تتعرف على مفهوم النظام المكاني أو الموضعي، حيث أن نفس الرمز يستخدم ليمثل أكثر من قيمة في العدد على حسب مكانه أو موضعه.
نظام العد العشري (النظام العشري - Decimal)
هو النظام المتعارف عليه والذي يستخدمه البشر للتعامل مع الأعداد (الأرقام)، ويمكن أن يتم تسمية هذا النظام بـ نظام الأعداد ذو رقم الأساس 10 وهو ترجمة للكلمة الإنجليزية Base 10، ونحن كبشر نستخدم هذا النظام يوميا سواء في عد النقود أو وزن المنتجات أو البضائع أو عد كمية من الأشياء والكثير من الإستخدامات لنظام العد العشري، من المؤكد أنك في مرحلة عمرية مبكرة قد درست كيفية التعامل مع الأعداد بإستخدام هذا النظام، وسوف أفترض أيضا أنك تعرف كيفية إجراء العمليات الحسابية من جمع وطرح وضرب وقسمة، وتعرف كيفية حساب الأس (Exponent)، تم تسمية هذا النظام بنظام العد العشري وذلك لأنه يستخدم عشرة رموز لتمثيل الأعداد (الأرقام).
ومن المتعارف عليه أن قيمة كل رمز تختلف بإختلاف مكانه (موضعه) في التمثيل العددي، فعلى سبيل المثال الرمز "1" في الرقم (1) يعبر عن وحدة واحدة، أما الرمز "1" في الرقم (10) فهو يعبر عن 1 مضروبا في 101 أي أنه يعبر عن عشرة وحدات، وبالتالي فإن كل رمز من الرموز العشرة تختلف قيمته بإختلاف المكان الذي يوجد به هذا الرمز، وهو ما يعرف بالإنجليزية بـ Significance of digit، وللتعرف أكثر على دلالة الأعداد سوف نقوم بتمثيل الرقم 2018.11 بالتفصيل، كالتالي
2018.11 = 2*103 + 0*102 + 1*101 + 8*100 + 1*10-1 + 1*10-22018.11 = 2*1000 + 0*100 + 1*10 + 8*1 + 1*0.1 + 1*0.012018.11 = 2000 + 0 + 10 + 8 + 0.1 + 0.01
ومن ذلك نستنتج أن قيمة أي رقم هي عبارة عن حاصل جمع كل رمز من رموز الرقم مضروبا في رقم الأساس مرفوعا لأس هو عبارة عن ترتيب الرمز في الرقم، والشكل التالي يوضح كيفية حساب قيمة الأس (ترتيب الرمز في الرقم)
كيفية التمييز بين الأرقام في الأنظمة العددية المختلفة؟
يوجد العديد من الطرق التي يتم إستخدامها لتمييز أي رقم بالنظام العددي التابع له، وذلك حتى نتمكن من التعامل مع الأرقام بالطريقة المناسبة، فإذا إفترضنا أننا نريد إجراء عملية الجمع التالية 1 + 1، فكيف يتم كتابة الرقم الناتج من عملية الجمع؟
بالطبع إن لم يكن لديك خلفية سابقة عن أنظمة العد المختلفة، فسوف تجيب بأن حاصل عملية الجمع هو الرقم 2، وذلك صحيح فقط إذا إفترضنا أن الرقمين هما من النظام العددي العشري، ولكن بالرجوع إلى الجدول في بداية المقال والذي يوضح الرموز المستخدمة في كل نظام عددي، سوف تجد أن الرمز "1" هو رمز مشترك بين جميع الأنظمة العددية، وبالتالي يجب توضيح النظام العددي لكل رقم نتعامل معه.
ولذلك سوف نقوم بوضع الرقم بداخل قوسين ثم نتبع القوسين برقم الأساس الخاص بالنظام العددي، مثال (10)10 وهو الرقم 10 (ما بداخل القوسين)، في النظام العشري (الرقم المكتوب بعد القوسين)، وعادة ما يتم كتابة رقم الأساس الخاص بـ النظام العددي التابع له الرقم بخط أصغر من المكتوب به الرقم، ويكون مكتوب أسفل الخط الموجود به الرقم، وتسمى هذه الطريقة في الكتابة بـ تحت بادئة - subscript.
ولتوضيح ذلك سوف نقوم بحل نفس المثال السابق في أكثر من نظام عددي
(1)10 + (1)10 = (2)10(1)2 + (1)2 = (10)2(1)3 + (1)3 = (2)3(1)8 + (1)8 = (2)8(1)16 + (1)16 = (2)16
بالطبع نحن لم نتطرق للعمليات الحسابية في الأنظمة العددية المختلفة حتى الآن، ولكني قمت بإستخدام هذا المثال تحديدا لتوضيح أن حاصل عملية الجمع بين رقمين يختلف بإختلاف النظام العددي المستخدم.
تحويل أي رقم من أي نظام عددي إلى نظام العد العشري
يوجد طريقة ثابتة لتحويل أي رقم من أي نظام عددي إلى النظام العشري، ويتم ذلك بإتباع الخطوات التالية
- نقوم بتحديد الدليل (قيمة الأس) - index، لكل خانة من خانات الرقم. ويتم ذلك بإستخدام الشكل السابق، والذي قمنا فيه بترتيب مكونات الرقم من العلامة الكسرية، حيث يتم تحديد القيمة 0 لأول رمز على يسار العلامة ثم نقوم بجمع الرقم 1 على الرمز السابق كلما إتجهنا إلى يسار العلامة (Integer)، ونطرح 1 من الرمز السابق كلما إتجهنا إلى يمين العلامة (Fraction).
- نقوم بضرب كل رمز من الرموز المكونة للرقم في رقم الأساس مرفوعا لـ الأس الذي حددناه في الخطوة السابقة، وهنا يجب مراعاة أن رقم الأساس هو الرقم الخاص بالرقم المراد تحويله، فإذا إفترضنا أننا نريد تحويل رقم من النظام الثنائي إلى النظام العشري فإن رقم الأساس المستخدم هو الرقم 2، وإذا أردنا التحويل من النظام الثماني فيكون رقم الأساس هو 8، وهكذا.
- نقوم بجمع الأرقام الناتجة من العملية السابقة، ويكون الناتج هو الرقم العشري.
ويمكننا إستنتاج القانون العام لتحويل أي رقم من أي نظام عددي إلى النظام العشري كالتالي
(dndn-1dn-2......d1d0.d-1d-2.....d-m)R = (dn * Rn + dn-1 * Rn-1 + ..... + d1 * R1 + d0 * R0 + d-1 * R-1 + d-2 * R-2 + ..... + d-m * R-m)10
وبتطبيق القاعدة العامة سوف نتمكن من حل الأمثلة التالية
1. ما هو الرقم العشري المرادف للرقم الثنائي (1011.01)2 ؟
(1011.01)2 = (1 * 23 + 0 * 22 + 1 * 21 + 1 * 20 + 0 * 2-1 + 1 * 2-2)10(1011.01)2 = (1 * 8 + 0 * 4 + 1 * 2 + 1 * 1 + 0 * 0.5 + 1 * 0.25)10(1011.01)2 = (11.25)10
2. ما هو الرقم العشري المرادف للرقم في النظام السادس عشر (A5.BC)16؟
(A5.BC)16 = (A * 161 + 5 * 160 + B * 16-1 + C * 16-2)10(A5.BC)16 = (10 * 161 + 5 * 160 + 11 * 16-1 + 12 * 16-2)10(A5.BC)16 = (10 * 16 + 5 * 1 + 11 * 0.0625 + 12 * 0.125)10(A5.BC)16 = (167.1875)10
تحويل أي رقم من النظام العشري إلى أي نظام عددي آخر
توجد أيضا طريقة أساسية لتحويل أي رقم من نظام العد العشري إلى أي نظام عددي آخر، وتتمثل في الخطوات التالية:
- يتم تقسيم الرقم إلى جزئين، وهما الرقم الصحيح (Integer) والجزء الكسري (Fraction).
- نقوم بتحديد رقم الأساس، وهو الرقم الخاص بالنظام العددي المراد التحويل إليه، على سبيل المثال إذا أردنا تحويل رقم عشري إلى النظام السادس عشر يكون رقم الأساس هو 16، وإذا أردنا التحويل إلى النظام الثماني يكون رقم الأساس هو 8، وهكذا.
- الرقم الصحيح
- نقوم بقسمة الرقم الصحيح على رقم الأساس.
- نأخذ الجزء الكسري من نتيجة حاصل القسمة ونقوم بضربه في رقم الأساس، لنحصل على رمز من مكونات الرقم.
- نكرر الخطوتين السابقتين حتى تصبح النتيجة تساوي صفر.
- نكتب الرموز التي حصلنا عليها بالترتيب من على يسار العلامة الكسرية.
- الرقم الكسري
- نقوم بضرب الرقم الكسري في رقم الأساس.
- نأخذ الرقم الصحيح الناتج من عملية الضرب، لنحصل على رمز من مكونات الرقم، (حتى إذا كان الرقم الصحيح هو صفر).
- نكرر الخطوتين السابقتين حتى تصبح النتيجة تساوي صفر، أو نكون قد حصلنا على عدد محدد من الرموز، (وهو ما يسمى بعملية التقريب للأرقام الكبيرة).
- نكتب الأرقام التي حصلنا عليها بالترتيب من على يمين العلامة الكسرية.
قد تبدو الخطوات للوهلة الأولى معقدة، ولكن حقيقة الأمر أنها خطوات بسيطة، وبمجرد تحويل أكثر من رقم بنفسك سوف تجدها سهلة وبسيطة، ونبدأ بحل مثال للتوضيح
ما هي قيمة الرقم العشري (11.25)10 في النظام الثنائي (???)2؟
| الرقم الصحيح - Integer | ||
|---|---|---|
| رقم الأساس | باقي القسمة الصحيح | باقي القسمة الكسري |
| 2 | 11 (11/2 = 5.5)=> 5 (5/2 = 2.5)=> 2 (2/2 = 1.0)=> 1 (1/2 = 0.5)=> 0 | --- (0.5 * 2)=> 1 (0.5 * 2)=> 1 (0.0 * 2)=> 0 (0.5 * 2)=> 1 |
| 1011. | ||
| الرقم الكسري - Fraction | ||
|---|---|---|
| رقم الأساس | باقي القسمة الكسري | باقي القسمة الصحيح |
| 2 | 0.25 (0.25*2 = 0.5)=> 0.5 (0.5*2 = 1.0)=> 0 | --- 0 1 |
| .01 | ||
وبذلك نحصل على الرقم الثنائي (1011.01)2، وبتطبيق نفس الخطوات يمكنك تحويل أي رقم عشري إلى رقم في أي نظام عددي آخر.


